Propiedades de las curvas de la indiferencia

Acabamos de construir las curvas de indiferencia, y no es casualidad que las representamos decrecientes y convexas: estas curvas tienen las siguientes propiedades:

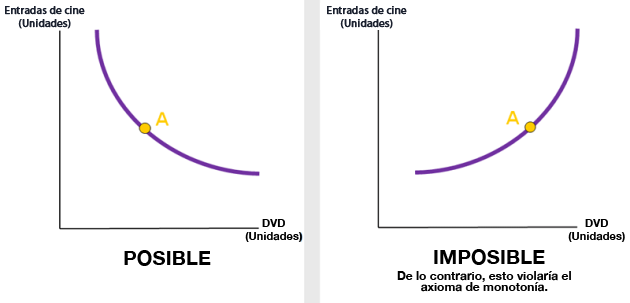
Las curvas de indiferencia son decrecientes:

Fundamental

Curvas de indiferencia decreciente

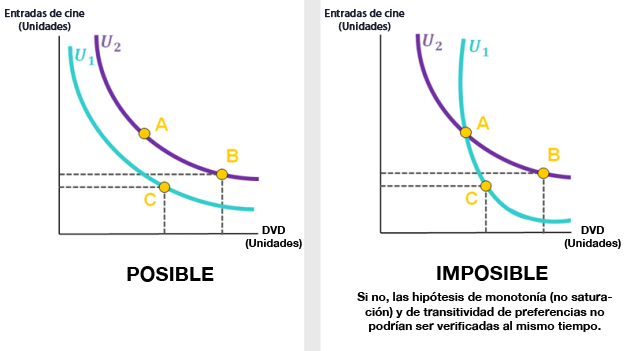
Las curvas de indiferencia no pueden cruzarse:

Fundamental

¿Curvas de indiferencia cruzadas?

Nota:

Remarcar

Generalmente, la pendiente de cada curva de indiferencia es cada vez más plana a medida que nos desplazamos hacia la derecha.

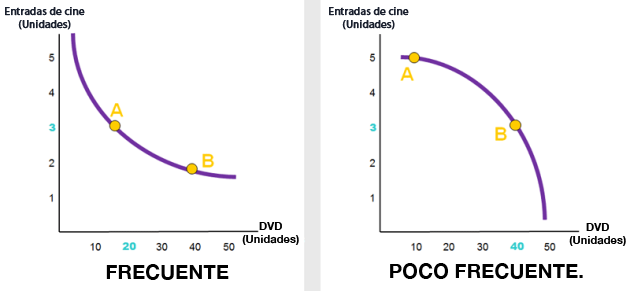
Preferencia por la diversidad

Preferencia por la diversidad:

 Ejemplo

Ejemplo de preferencia por la diversidad

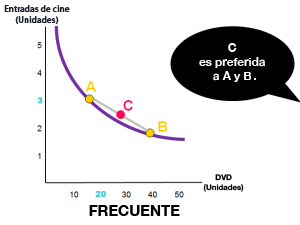
Toda canasta C que contiene:

• Una proporción a un número de DVD de la canasta A y (1 – a) de la canasta B (a pertenece [0,1])
• Una proporción a un número de lugares de cine de la canasta A y (1 – a) de la canasta B

C es preferida o indiferente a las canastas A y B.